El problema de Monty Hall.
El problema de Monty Hall o paradoja de Monty Hall, muy reconocido gracias a la controvercia que causo Marilyn Vos Savant a través de su propuesta de solucion. Éste es un problema matemático estadístico de probabilidades basado en el concurso televisivo estadounidense Let’s Make a Deal (Trato hecho).
Este concurso (como la gran mayoría) están enfocados a la entretención donde los participantes pueden llevar a sus casas un gran premio en dinero.
Este consiste en que el presentador te presenta tres puertas cerradas. Detrás de una de ellas, se encuentra un gran premio en dinero o en ocasiones era un coche nuevo y reluciente. Detrás de las otras dos puertas sólo se encuentran cabras (si cabras).
El anfitrión te pide que elijas una de las 3 puertas y es cuando comienza el problema real, supongamos que seleccionas la puerta N°1, luego, el anfitrión, que conoce la respuesta, abre por ejemplo la puerta N°3, revelando una de las cabras (ósea una de las puertas equivocada). “Ahora”, dice, volviéndose hacia el participante “¿quieres mantener la puerta N°1 o quieres cambiar a la puerta N°2?”, esta es la primicia de la paradoja o problema de Monty Hall.
El problema fue planteado y resuelto por el matemático Steve Selvin en la revista American Statistician en 1975 y posteriormente popularizado por Marilyn vos Savant en Parade Magazine en 1990. El problema fue bautizado con el nombre del presentador de dicho concurso, Monty Hall.
El 9 de septiembre de 1990, Savant publicó en su columna el problema planteado y resuelto en 1975 por el estadístico experto en probabilidades estadounidense Steve Selvin, con la siguiente pregunta:
“Imagínese que está participando a un programa de concursos y que tiene que escoger entre tres puertas”.
El trato hacia ella no fue el mejor de todos y la misma revista le solicito que por favor aclarara su error ya que estaban llegando muchos reclamos a la revista insultando que si de verdad era una mujer inteligente, extremo que llego a aparecer en el New York Time. Se tardo dos publicaciones para que los lectores y científicos de la época le creyeran y sobre todo lograran entender.
Solución del problema de Monty Hall o paradoja de Monty Hall.
La premisa del problema es ¿Debe el participante cambiar de puerta o debe mantener la primera elección?
La solución se basa en tres suposiciones básicas:
- El presentador siempre abre una puerta.
- Tras la que el presentador ha abierto siempre hay una cabra, puesto que conoce lo que hay detrás de cada puerta.
- El presentador la escoge entre las dos restantes después de que el concursante haya escogido la suya.
Teniendo esto en cuenta las probabilidades aumentan a favor del concursante si el CAMBIA SU OPCIÓN.
A continuación, está la explicación de porque aumentan las probabilidades de ganar:
El pensamiento erróneo al pensar en este problema es que cuando queden dos puertas ambas tienen la misma probabilidad ósea 1 sobre 2 (1/2) de contener el fabuloso automóvil reluciente. Pero esta suposición es errónea ya que el conductor abre la puerta después de la elección del jugador. Por lo tanto, la elección del jugador si o si afectara a la puerta que abre el conductor, no es al azar la puerta qué el abre.
Ahora si el participante justo escoge en su primera opción la puerta en la que se encuentra el gran premio estamos hablando de una probabilidad de 1 sobre 3 (1/3), por lo que el presentador podría abrir cualquier puerta.
Esto recae en que obviamente el jugador pierde el premio si cambia cuando se le ofrece la oportunidad, puesto que había acertado.
Si por el contrario el jugador escoge una cabra en su primera opción que seria una probabilidad de 2 sobre 3 (2/3), el conductor solo tiene una opción de puerta para abrir, y esta es la única puerta restante que contiene la cabra. Por conclusión la puerta restante tendrá que contener el premio, por lo que al cambiar la opción se gana.
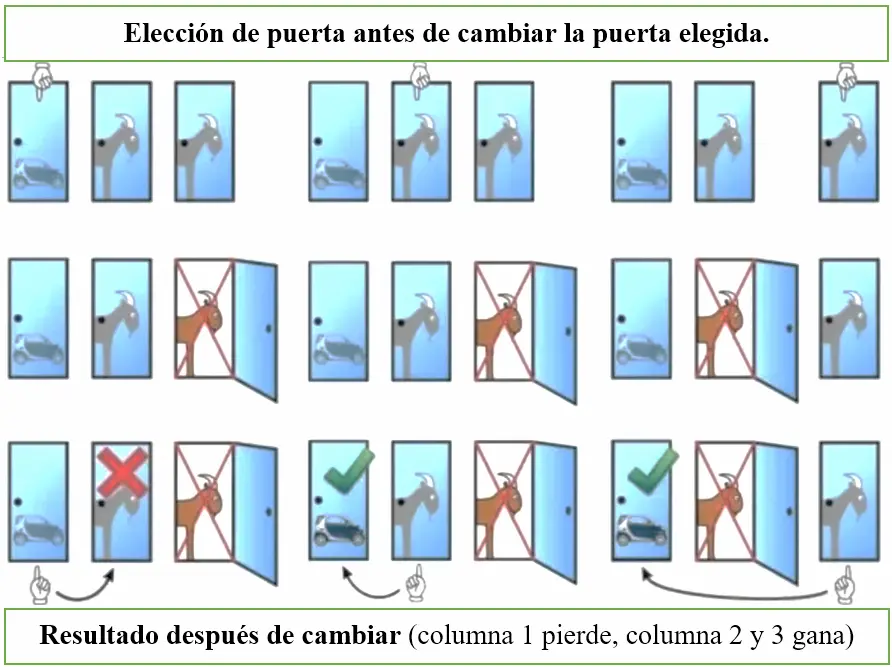
Solución grafica al problema de Monty Hall.
A continuacion encontrras en la imagen un resumen visual de los resultadosobtenidos dependiendo de la puerta que elijas al comenzar el concurso.
En resumen:
- Si a la primera se gana hablamos de una probabilidad de 1 sobre 3 opciones.
- Si a la primera le apunta a la cabra la probabilidad es de 2 sobre 3 opciones.
Por este motivo siempre el concursante debe cambiar la elección si quiere maximizar las probabilidades de ganar.




0 comentarios