The problem of Monty Hall

The problem of Monty Hall.

The problema de Monty Hall o paradoja de Monty Hall, muy reconocido gracias a la controvercia que causo Marilyn Vos Savant a través de su propuesta de solucion. Éste es un problema matemático estadístico de probabilidades basado en el concurso televisivo estadounidense Let's Make a Deal (got a Deal).

This contest (as the vast majority) are focused on the entertainment where the participants can take home a large cash award.

This is that the presenter presents you three closed doors. Behind one of them, there is a big prize money or sometimes it was a new car and shiny. Behind the other two doors are only goats (if goats).

The host asks you to choose one of the 3 doors and starts the real problem, suppose that you select the door N°1, then the host, who knows the answer, opens, for example, the door N°3, revealing a goat (bone one of the doors wrong). “Now,” he says, turning towards the participant “do you want to keep the door N°1, or you want to switch to door No. 2?”, this is the premise of the paradox or problem Monty Hall.

The problem was posed and solved by the mathematician Steve Selvin in the journal the American Statistician in 1975 and later popularized by Marilyn vos Savant in Parade Magazine in 1990. The problem was baptized with the name of the presenter of the contest, Monty Hall.

On September 9, 1990, Savant published in his column for the problem posed and solved in 1975 by the statistical expert in odds american Steve Selvin, with the following question:

“Imagine that you are participating in a program of contests and has to choose between three doors.”

The treatment towards her was not the best of all and the same magazine I ask you to please clarify their error as they were reaching many claims to the magazine insulting that if you really was a smart woman, end that I get to appear in the New York times. It takes me two publications for the readers and scientists of the time we think, and above all, to achieve understanding.

Solution of the problem of Monty Hall or paradox, Monty Hall.

The premise of the problem is what Should the participant change of gate or you must keep the first choice?

The solution is based on three basic assumptions:

1. The host always opens a door.
2. After that the presenter has opened up there's always a goat, because who knows what is behind each door.
3. The presenter chooses between the two remaining after the contestant has chosen theirs.

Taking this into account, the odds increase to the benefit of the contestant if the CHANGE YOUR OPTION.

Then, is the explanation of because they increase the odds of winning:

The faulty thinking in thinking about this problem is that when there are two doors both have the same probability bone 1 on 2 (1/2) contain the fabulous car sparkling. But this assumption is erroneous, as the driver opens the door after the choice of the player. Therefore, the choice of the player whether or affect the door that opens to the driver, is not random, the door does open.

Now if the participant just choose in your first choice the door on which is located the grand prize we're talking about a probability of 1 of 3 (1/3), so that the presenter could open any door.

This falls in that obviously the player loses the prize if you change when you are offered the opportunity, as she had guessed.

On the contrary, if the player picks a goat in his first option would be a probability of 2 over 3 (2/3), all the driver has a choice of door to open, and this is the only gate remaining that contains the goat. In conclusion, the door remaining will have to contain the prize, so that when you change the option wins.

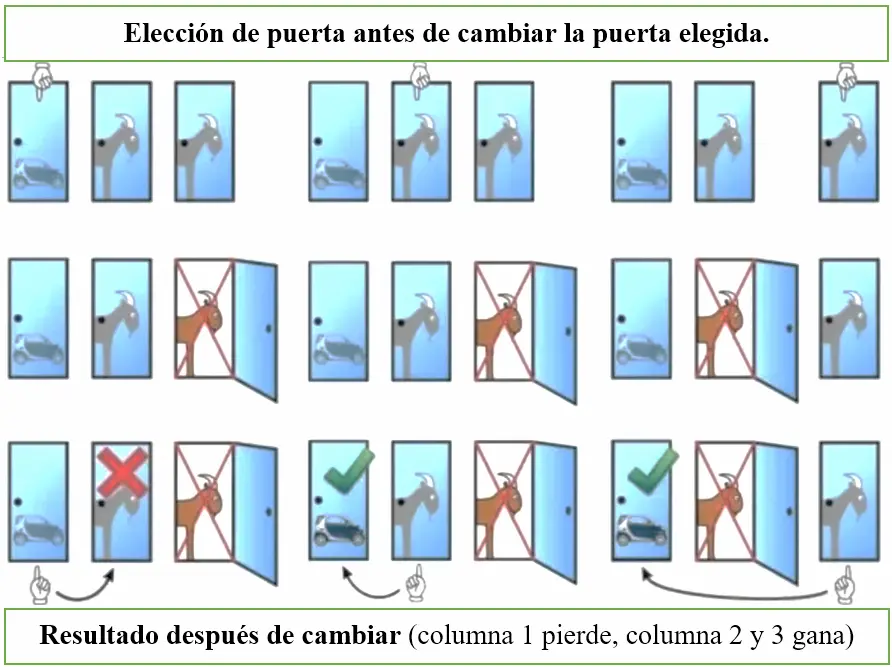
Solution graph the problem and Monty Hall.

Below encontrras in the picture a visual summary of the resultadosobtenidos depending on the door you choose at the start of the contest.

In summary:

• If the first wins, we speak of a probability of 1 out of 3 options.
• If the first aims at the goat the probability is 2 over 3 options.

Por este motivo siempre el concursante debe cambiar la elección si quiere maximizar las probabilidades de ganar.